[Paradoxe] Quelle est la probabilité.....
Quelle est la probabilité..... [Paradoxe] - Sciences - Discussions
Marsh Posté le 11-10-2005 à 19:43:12
1ere bonne réponse...mais ils y en a d'autre parceque c'est un paradoxe....
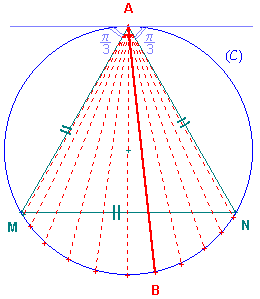
Par raison de symétrie, nous pouvons supposer que l'une des extrémités de la corde a été fixée en un point A choisi aléatoirement sur le cercle (C).
L'autre extrémité B sera choisie au hasard sur la circonférence.
La probabilité que le point B tombe sur un arc donné de la circonférence étant proportionnelle à la longueur de cet arc, la corde est plus longue que le côté [MN] du triangle équilatéral inscrit dans le cercle lorsque B se trouve sur l'arc arc MN dont la longueur est le tiers de celle de la circonférence du cercle (C).
En conséquence, B devra être choisi sur l'arc de cercle opposé sous-tendu par le côté du triangle équilatéral inscrit.
Puisque le triangle équilatéral, tout comme le sommet A, détermine trois arcs isométriques, la probabilité P cherchée est :
P=1/3.
Message édité par Profil supprimé le 11-10-2005 à 20:02:18
Marsh Posté le 11-10-2005 à 19:45:49
Problème mal posé, ça dépend comment tu définis "tirer une corde au hasard".
cas 1 : on choisit de façon équiprobable deux points sur le cercle, qui définissent les deux extrêmités de la corde
cas 2 : on choisit un point P de façon équiprobable à l'intérieur du cercle. La corde est le seul segment [AB], avec A et B sur le cercle et P le milieu de [AB]
Tu trouveras un résultat différent dans les deux cas et pourtant ils répondent tous les deux au problème ![]()
Marsh Posté le 11-10-2005 à 19:49:23
Dans les deux cas que j'ai proposé, de tête ça doit être 1/3 et 1/4, mais avec des définitions un minimum tordues, on doit pouvoir atteindre toutes les valeurs entre 0 et 1
Marsh Posté le 11-10-2005 à 19:53:02
2eme bonne réponse
mais le calcul se fait difficilement de tete pour cette solution ![]() tu doit connaitre le paradoxe de tete
tu doit connaitre le paradoxe de tete
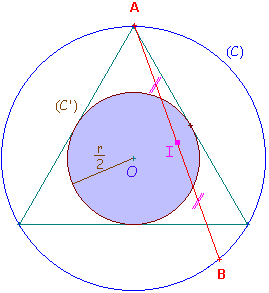
La longueur de la corde [AB] est déterminée par la position de son milieu I. Choisir une telle corde revient donc à se donner un point au hasard à l'intérieur du cercle.
La probabilité que la longueur de la corde soit supérieure à celle du côté du triangle équilatéral inscrit est alors égale à la probabilité que le milieu de la corde soit intérieur au cercle (C') de rayon moitié, inscrit dans ce triangle.
En effet, la distance du milieu I de la corde au centre O du cercle ne doit pas excéder le rayon du cercle (C').
Si r est la longueur du rayon de (C), celle du rayon du cercle (C') commun à tous les triangles équilatéraux inscrits est r/2.
Le centre de la corde devra donc se trouver dans le cercle colorié en violet sur le schéma.
La répartition de ce point étant uniforme dans le cercle, la probabilité demandée est le rapport entre l'aire du cercle (C') et l'aire du cercle (C).
D'où la probabilité demandée :
P = 1/4.
Message édité par Profil supprimé le 11-10-2005 à 20:02:04
Marsh Posté le 11-10-2005 à 19:55:55
| Svenn a écrit : Dans les deux cas que j'ai proposé, de tête ça doit être 1/3 et 1/4, mais avec des définitions un minimum tordues, on doit pouvoir atteindre toutes les valeurs entre 0 et 1 |
Par exemple, on choisit de façon équiprobable n points à l'intérieur du cercle, et on garde le plus au centre (ou le plus à l'extérieur) qui devient le milieu de la corde. En jouant sur le nombre n, on peut s'approcher de 0 ou de 1 autant que l'on veut ![]()
Marsh Posté le 11-10-2005 à 19:56:34
ReplyMarsh Posté le 11-10-2005 à 19:58:04
| ploop a écrit : Wow |
Et si, le problème n'est pas parfaitement défini contrairement aux apparences ![]()
Marsh Posté le 11-10-2005 à 19:59:27
| Svenn a écrit : mais avec des définitions un minimum tordues, on doit pouvoir atteindre toutes les valeurs entre 0 et 1 |
non quand même pas....plusieurs certes mais pas une infinité
Marsh Posté le 11-10-2005 à 20:01:06
La troisieme solution
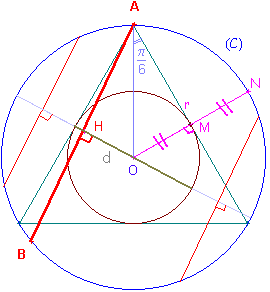
La longueur de la corde [AB] est caractérisée par sa distance d au centre O du cercle (C).
La distance maximale que peut atteindre d pour que la longueur de la corde soit supérieure à celle du côté du triangle équilatéral inscrit, est la longueur OM. Tant que d < OM, la corde tracée vérifie donc les conditions du problème.
Le rayon du cercle (C) étant r, nous avons :
OM = r/2.
Donc les côtés d'un triangle équilatéral inscrit dans (C) sont situés à une distance r/2 du centre O du cercle, par invariance de cette distance par des rotations de centre O d'un triangle équilatéral ainsi donné.
Par suite, la distance d de la corde [AB] au centre du cercle ne devra pas excéder r/2, distance du centre O aux côtés d'un triangle équilatéral inscrit dans le cercle.
Si nous considérons le diamètre perpendiculaire à ces cordes toutes parallèles à [AB] dans notre exemple , leur milieu H doit appartenir à un segment dont la longueur est 2 × d = r, et qui appartient à un diamètre du cercle (C), de longueur 2r.
Ce raisonnement étant valable pour toutes les directions, cette condition se généralise parfaitement.
Or la distance maximale d'une corde est r, d'où la probabilité P recherchée :
P = 1/2.
Message édité par Profil supprimé le 11-10-2005 à 20:01:42
Marsh Posté le 11-10-2005 à 20:02:01
Si, le protocole de "choix au hasard d'une corde" que j'ai donné plus haut est parfaitement rigoureux ![]()
Marsh Posté le 11-10-2005 à 20:05:13
On peut au moins atteindre toutes les valeurs 0,25^n et 1-0,75^n, avec n dans N*, ça fait déjà pas loin d'une infinité
Marsh Posté le 11-10-2005 à 20:07:12
| Svenn a écrit : Dans les deux cas que j'ai proposé, de tête ça doit être 1/3 et 1/4, |
1/4 de tete ce n'est pas possible à moins d'avoir un calculateur dans la tete....regardes la formule sur cette page..alors de tête je doute de ta franchise...tu connaissais ce paradoxe qui est la paradoxe de Bertrand
http://www.trigofacile.com/maths/c [...] roche3.htm
http://www.trigofacile.com/maths/c [...] rtrand.htm
Le paradoxe mis à jour par Joseph Bertrand révèle les limites du recours à l'intuition en probabilités
Message édité par Profil supprimé le 11-10-2005 à 20:09:56
Marsh Posté le 11-10-2005 à 20:09:39
Enfin, y a pas besoin de lancer Excel pour se rendre compte qu'un cercle de rayon R/2 a une aire 4 fois plus faible que celle d'un cercle de rayon R ![[:airforceone] [:airforceone]](https://forum-images.hardware.fr/images/perso/airforceone.gif)
Marsh Posté le 11-10-2005 à 20:13:46
| Svenn a écrit : On peut au moins atteindre toutes les valeurs 0,25^n et 1-0,75^n, avec n dans N*, ça fait déjà pas loin d'une infinité |
il y a 4 méthodes a priori....peut-etre en as tu d'autres a proposer ?
Marsh Posté le 11-10-2005 à 20:25:47
La méthode que j'ai proposée dans le 8eme post de ce topic ne fait pas partie des 4 de ce site et permet d'arriver à 0.25^n ou 1-0.75^n
Et avec un tout petit peu d'imagination on devrait pouvoir arriver à tous les réels de l'intervalle [0;1].
Marsh Posté le 11-10-2005 à 20:28:20
le paradoxe par l'animation ..et tres bien décrit..
http://perso.wanadoo.fr/therese.ev [...] rtrand.htm
Marsh Posté le 11-10-2005 à 20:30:46
Très sympa comme topic, merci phobos72 ![]()
Instinctivement j'avais pensé 1/2 ![]()
Marsh Posté le 11-10-2005 à 20:32:26
c'est moins paradoxal que ca n'y parait, il suffit de definir clairement ce qu'est "tirer une corde au hasard"
pour moi "au hasard" signifie "totalement aleatoirement sans direction imposee ou autre contrainte...."
j'aurais du dire 1/2 alors ? ![]()
Message édité par ploop le 11-10-2005 à 20:33:23
Marsh Posté le 11-10-2005 à 20:34:17
C'est à dire ? deux points du cercle au hasard ? ou un point/un angle au hasard ? ou autre chose ?
/edit : Svenn ma griller. ![[:jascooby] [:jascooby]](https://forum-images.hardware.fr/images/perso/jascooby.gif)
Message édité par hephaestos le 11-10-2005 à 20:34:58
Marsh Posté le 11-10-2005 à 20:35:39
je cite l'auteur du dernier lien:
| Citation : Il s'agit d'un choix de conditions qui conduisent à des évènements différents. Le problème est simplement mal posé : l'expression "choisir au hasard une corde dans un cercle" n'a pas d'interprétation unique. |
Marsh Posté le 11-10-2005 à 20:38:51
| ploop a écrit : |
Oui, intuitivement, au hasard ça veut juste dire 'tout est possible'. Mais là, on demande un résultat qui est une probabilité, donc il faut caractériser le hasard en terme de probabilités.
Marsh Posté le 14-10-2005 à 20:19:14
Moi je fais comme ça :
Je part d'un point au hasard (ni en A , ni en B , ni en C )
Je joint ce point a un autre point de manière a ce que la distance soit de racine(3)* R
( le triangle inscrit a des cotés de racine(3)* le rayon du cercle )
Il ne reste plus qu'a determiner respectivement la longueur de la corde delimitée par nos 2 points (s1 = 2*pi/3*r ) et la longueur de la corde qui delimite le diametre ( s2=pi*r)
La probabilité cherchée est : (s2-s1)/s2 = 1/3 ![]()
Marsh Posté le 14-10-2005 à 22:22:08
J'ai survolé le topic et je suis tombé sur la conclusion que la proba était de 1 sur 3, en partant de la caractérisation d'une corde par l'angle fait avec la tangente au premier point d'intersection.
La caractérisation par la position du point milieu de la corde ne me semble pas correcte. En partant du point milieu de la corde, on ne décrit pas un disque mais une portion de courbe (tous les point du disque représentant 1/4 du disque ne peuvent pas être atteints par cette méthode).
La méthode qui aboutit à 1 chance sur 2 me semble en revanche plus dérangeante. Si je comprend bien, le problème est que le protocole de choix n'est pas équivalent selon que l'on choisi la distance au milieu du cercle ou l'angle avec la tangente. C'est ça ?
En considérant une répartition selon une loi normale sur la distance au centre du disque, on ne retombe pas sur la même loi de répartition en considérant les angles. C'est ça, le paradoxe ?
---------------
La ligne droite n'est en aucun cas le plus court chemin entre deux points. Sauf, bien sûr, si les deux points sont bien alignés l'un en face de l'autre
Marsh Posté le 14-10-2005 à 22:32:02
Putain comment j'ai bien fait de pas faire une prépa après le bac ![[:mlc] [:mlc]](https://forum-images.hardware.fr/images/perso/mlc.gif)
Marsh Posté le 14-10-2005 à 22:36:21
Une fois qu'on le saura, on sera vachement avancés faut dire ![]()
Marsh Posté le 15-10-2005 à 08:38:37
| Prozac a écrit : J'ai survolé le topic et je suis tombé sur la conclusion que la proba était de 1 sur 3, en partant de la caractérisation d'une corde par l'angle fait avec la tangente au premier point d'intersection. |
C'est ma méthode qu'est la bonne car la plus générale .
il n'y a pas de paradoxe . ![]()
Marsh Posté le 15-10-2005 à 09:10:30
ReplyMarsh Posté le 15-10-2005 à 10:06:35
Non non, il y a effectivement paradoxe. La méthode de construction par distance ou angle ne sont pas équivalente mais toutes les deux conformes à un tracé aléatoire. Seulement les lois de distributions ne sont pas les mêmes.
La méthode qui parvient à une proba de 1/2 me semble effectivement mauvaise. Prend un corde faite à partir d'un point du disque. Toutes les cordes construites à partir de segments dont le centre est sur la première corde sont strictement la même. Comme la section du disque est plus grande à mesure qu'on se rapproche du centre, la probabilité qu'on tape vers le centre (donc une corde supérieure au côté du triangle) est plus forte.
Le choix de l'angle à la tangente ou de la distance au centre me semblent en revanche correcte. Mais si tu balaies les possibilités, par exemple par incréments de 1mm sur la figure (donc de manière régulière), les angles par rapport à la tangente des cordes ainsi créées seront plus serrés vers l'extérieur que vers l'interieur. C'est clair ? Il y a des démonstrations possibles mais c'est juste pour pouvoir visualiser simplement l'affaire. Le lien entre l'angle et la distance au centre doit suivre l'évolution de la fonction tangente, non linéaire.
A l'inverse, si on balaie les possibilités de l'angle (par exemple par incrément de 1°), on arrivera à des incréments plus grand pour les angles faibles, plus grands à mesure qu'on se rapproche d'un angle droit par rapport à la tangente.
Dont si on prend un domaine qui regroupe x% du domaine de toutes les solutions dans une méthode, on tombera sur un domaine regroupant y% de toutes les solutions.
Choisir une distance au centre amènera à favoriser les angles les plus éloignés de la perpendiculaire car les 5% de solutions sur les angles des cordes plus courtes vont aboutir à un domaine sur les angles couvrant y%, avec y>5.
Avec une image, ça irait mieux, mais c'est peut être déjà suffisant, non ?
Message édité par Prozac le 15-10-2005 à 10:09:56
---------------
La ligne droite n'est en aucun cas le plus court chemin entre deux points. Sauf, bien sûr, si les deux points sont bien alignés l'un en face de l'autre
Marsh Posté le 15-10-2005 à 11:28:31
| hephaestos a écrit : Euh, source ? |
La source est contenue dans la démonstration :
Je prend un point n'importe ou sur le cercle , je relie ce point a un autre situé a une distance de racine(3)* R .
Reste plus qu'a determiner le rapport des cordes ( (s2-s1)/s2.
Si on fait une simulation informatique, je suis a peu prés sur que statistiquement on vérifie cette probabilité ( depend juste du generateur de nombres aléatoire)
En fait, a partir du moment ou tu choisis ton point, tout est parfaitement determiné .
Message édité par le penseur fou le 15-10-2005 à 11:30:47
Marsh Posté le 15-10-2005 à 11:34:49
| le penseur fou a écrit : C'est ma méthode qu'est la bonne car la plus générale . |
En quoi cette méthode est plus générale que les autres ? Toutes les méthodes décrites sur cette page répondent parfaitement à la question posée ![]()
Marsh Posté le 15-10-2005 à 12:10:10
| le penseur fou a écrit : La source est contenue dans la démonstration : |
la pertinence de ta méthode dépend de la méthode pour évaluer l'erraticité de la distribution.
En choisissant au hasard l'angle avec la tangente, on pourra me reprocher de favoriser les cordes les plus proches du centre du cercle. Et donc de biaiser d'une certaine manière le résultat. C'est pourtant sans doute cette méthode qui sera la plus pertinente par exemple pour un problème de balistique (par exemple pour travailler sur la forme d'un stade de lancement du marteau). Faites pas chier, on va dire que le lanceur a les yeux bandés et ne peut pas viser et que tous les angles de départ sont équiprobables ![]() .
.
Réciproquement en choisissant la distance au centre, on pourra me reprocher de favoriser les cordes les plus éloignées du centre. C'est par contre la méthode la plus pertinente si par exemple je devais calculer la probabilité qu'une barre de métal de la longueur du côté du triangle puisse passer à travers un cercle (le problème est encore plus idiot mais c'est pour l'exemple).
Les deux méthodes sont correctes et cohérentes avec l'énoncé. Elles sont contradictoires parce que l'énoncé n'est pas assez précis et ne ferme pas le problème à 1 et 1 seule solution.
Message édité par Prozac le 15-10-2005 à 12:12:58
---------------
La ligne droite n'est en aucun cas le plus court chemin entre deux points. Sauf, bien sûr, si les deux points sont bien alignés l'un en face de l'autre
Marsh Posté le 15-10-2005 à 12:51:56
| le penseur fou a écrit : La source est contenue dans la démonstration : |
Ce que je critique, c'est que tu qualifies ta méthode de 'générale', alors qu'elle n'a rien de générale. D'ailleurs, je veux bien savoir précisément ce que tu entends par 'général'.
Marsh Posté le 15-10-2005 à 13:06:49
Le site d'où sortent les illustrations : http://www.trigofacile.com/maths/curiosite/index.htm
---------------
La ligne droite n'est en aucun cas le plus court chemin entre deux points. Sauf, bien sûr, si les deux points sont bien alignés l'un en face de l'autre
Marsh Posté le 15-10-2005 à 19:49:42
| hephaestos a écrit : Ce que je critique, c'est que tu qualifies ta méthode de 'générale', alors qu'elle n'a rien de générale. D'ailleurs, je veux bien savoir précisément ce que tu entends par 'général'. |
Une petite simulation informatique te convaincrait-elle ?
Au sein d'une boucle de 1000000 iterations,Je prend 2 points au hasard sur le cercle:
angle1:=random*2*pi ; angle2:=random*2*pi;
x1:=r*cos(angle1); x2:=r*cos(angle2);
y1:=r*sin(angle1); y2:=r*sin(angle2);
je mesure leur distance : d:=racine ( (x1-x2)^2 + (y1-y2^)^2 )
je regarde si elle est superieure ou egale a racine(3)*r , si oui je compte (total:=total +1)
a la fin de la boucle la probabilité est de: total/1000000 = 1/3
Donc pas de paradoxe on obtient toujours le meme resultat .
[ racine(3)*r, c'est la longueur des cotés du triangle equilatéral, bien entendu ]
Marsh Posté le 15-10-2005 à 20:33:45
| le penseur fou a écrit : Une petite simulation informatique te convaincrait-elle ? |
Tu ne réponds toujours pas à la question : en quoi ce mode de détermination d'une corde aléatoire est-il plus général qu'un autre (par exemple, choisir aléatoirement un point dans le disque qui sera le milieu de notre corde) ?
Sujets relatifs:
- Probabilité de traverser un mur
- Paradoxe des suppléments vitaminiques...?
- Paradoxe francais ?
- [matheux, probabilité] combien de temps l'homme vas survivre ?
- Le paradoxe de Fermi
- "Le prix indiqué tient compte de la réduction" [PARADOXE]
- La probabilité de mesurer une température de 0K dans le vide est elle
- probabilité

Marsh Posté le 11-10-2005 à 19:35:54
Considérons un triangle équilatéral et son cercle circonscrit. On tire une corde au hasard. Quelle est la probabilité que sa longueur soit supérieure à celle du côté du triangle ?


A vous de jouer...
solutions par plusieurs animations plus bas dans la page....
Message édité par Profil supprimé le 11-10-2005 à 20:30:03