Afficher une grille dans GoogleEarth à partir d'un point
Afficher une grille dans GoogleEarth à partir d'un point - Algo - Programmation
Marsh Posté le 08-03-2017 à 17:06:15
Pour moi ça dépend de la latitude.
Un algo rapide http://gis.stackexchange.com/quest [...] -of-meters
| Citation : If your displacements aren't too great (less than a few kilometers) and you're not right at the poles, use the quick and dirty estimate that 111,111 meters (111.111 km) in the y direction is 1 degree (of latitude) and 111,111 * cos(latitude) meters in the x direction is 1 degree (of longitude). |
---------------
sheep++
Marsh Posté le 08-03-2017 à 17:11:15
Bonjour !
Je dois rater une subtilité (je considère la terre sphérique ? Je ne tiens pas compte de la projection ?), mais je me lance quand même ...
Si on calcule les steps en degrés, on devrait avoir (en mètres):
un degré longitude = (circonférence de la terre / 360)*cos(latitude)
un degré latitude = (circonférence de la terre / 360)
Et donc, pour un tout petit "radius", et si le rectangle n'est pas trop près d'un pôle ...
step latitude = radius / degré latitude (en degré)
step longitude = radius / degré longitude.
En étant trop proche du pôle, on doit pouvoir adapter assez facilement les formules en faisant un changement de repère.
Mais j'ai vraiment l'impression d'enfoncer une porte ouverte et de passer à côté de la difficulté, auquel cas, désolé ![]()
Edit : grillé ! Mais on donne tous les deux les mêmes formules (en considérant que la circonférence est de 40 000 km) ![]()
Edit 2 : après réflexion, ce n'est pas tout à fait un rectangle, car le point à l'opposé de notre point de départ est légèrement faux (les deux autres sont bons, en revanche), mais pour des petites valeurs du radius (petites par rapport à la longueur du degré de longitude), cela reste très acceptable (il faudrait prendre pour le point à l'opposé le cosinus de la latitude du point + déplacement en latitude), le trapèze ressemble encore pas mal à un rectangle ![]() .
.
Message édité par Farian le 08-03-2017 à 17:19:16
---------------
On n'est jamais très fort pour ce calcul !
Marsh Posté le 08-03-2017 à 18:09:52
Moi, j'avais trouvé ce site : https://www.developpez.net/forums/d [...] raphiques/
$UN_KM_EN_LAT = (90/10000);
// Longueur maximale en degré pour la latitude
$max_dist_lat = ($UN_KM_EN_LAT * $dist_km);
// Longueur maximale en degré pour la longitude
$max_dist_long = ((360*$dist_km)/(40000 * cos(deg2rad($latitude))));
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 08-03-2017 à 19:45:50
Je suis tombé sur ça : http://msi.nga.mil/MSISiteContent/ [...] egree.html
Calcul dispo dans le code source de la page, je n'ai pas testé et encore moins vérifié ce que ça donnait.
Message édité par MaybeEijOrNot le 08-03-2017 à 19:46:18
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 09-03-2017 à 12:15:19
Purée, je galère. ![]() J'ai des petits décalages de 20 à 50m
J'ai des petits décalages de 20 à 50m ![]()
En gros, j'ai un rectangle initial repéré par ses 4 coins (LatMin, LatMax, LngMin, LngMax). Je veux découper ce rectangle en cellules de x mètres de côté. A l'intérieur de ce rectangle, j'ai des points repérés par leurs coordonnées. Je veux compter le nb de points par cellule. Pour savoir dans quelle cellule se trouve un point, je calcule le n° de ligne et de colonne de la cellule dans la grille.
Voici mon code. $BoundBox contient les coordonnées des 4 coins de ma zone à découper en cellules.
Code :
|
La table grid contient numline, numcol (n° de ligne et colonne de la cellule), lat, lng (coordonnées du centre de la cellule) et NB (nb points dans la cellule). La table points contient lat, lng (coordonnées du point).
Pour trouver dans quelle cellule se trouve un point, je fais la [lat du point - lat du coin min de la zone] / pas calculé pour la latitude. Ca me donne le n° de ligne. Je fais le même calcul pour la longitude. Je pense que c'est dans ce calcul que j'ai un pb. Je dois pas affecter les points aux bonnes cellules, d'où le décalage visuel entre mes cellules qui doivent avoir le plus de points et l'endroit où se trouvent réellement ces points.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 09-03-2017 à 13:41:20
Et il fait quelle taille ton rectangle? Ceci est déterminant sur le fait qu'on puisse considérer ou non qu'un degré de latitude et/ou longitude est constant sur toute la surface de ton rectangle. Il faut vérifier que la variation (entre ton coin supérieur gauche et inférieur droite) d'un degré converti en mètre est négligeable par rapport à la taille de ton pas.
Cela dépend donc de la taille de ton pas, de la taille de ton rectangle et de ta formule de conversion (qui peut être plus ou moins précise).
Pour moi le calcul coordonnées du point moins coordonnées de ton coin et le tout divisé par ton pas est la bonne méthode. Après en faisant ainsi tu minimises l'erreur en haut à gauche de ton rectangle et la maximise en bas à droite mais si tu peux te le permettre autant ne pas se prendre la tête.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 09-03-2017 à 13:53:26
Mon rectangle (qui est en fait un carré) peut faire jusqu'à 111 km de côté (30 NM de part et d'autre d'un point central en fait).
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 09-03-2017 à 17:18:11
Oui donc en fonction du modèle de conversion choisi ça ne me paraît pas aberrant d'avoir des erreurs de plusieurs dizaines de mètres.
Et de ce que je vois tu te bases sur un modèle sphérique, je pense que tu ne peux plus faire une telle approximation vu la précision demandée. Regarde dans le lien que j'ai mis le calcul utilisé. Je ne sais pas sur quel modèle il se base mais il sera déjà plus correct.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 09-03-2017 à 17:44:31
D'ailleurs, avec les chiffres de wikipedia, si je fais un calcul de l'erreur commise à une latitude de 45° en partant sur une approximation affine de la variation de la circonférence réelle de la terre (passant par les pôles) entre une latitude de 30 et 45° on trouve 19m de différence sur 111km entre le modèle sphérique et réel.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 09-03-2017 à 18:38:54
Une autre façon de faire serait de mesurer combien de fois tu loge ta grille dans ton carré en longitude(Nlong) et en latitude (Nlat). Pour faire ça tu utilise l'approximation soit sur deux côté du carré, soit sur les médianes.
Ensuite tu calcule le pas d'angle en longitude pour ta grille (arc longitude de ton carré / Nlat).
Puis en itératif tu détermines l'angle de chaque latitude de ta grille.
Enfin pour chaque latitude tu détermine le pas d'angle en longitude et tu itères pour chaque point sur ta latitude.
Avec cet méthode tu dilues l'erreur dans chaque carré au lieu de s'accumuler.
Je sais pas si c'est clair.
Message édité par h3bus le 09-03-2017 à 18:43:32
---------------
sheep++
Marsh Posté le 09-03-2017 à 19:22:26
De toute façon, à moins de faire tes calculs selon le modèle WGS84, tu auras toujours une "erreur". Après c'est toi qui voit si c'est acceptable ou non. Cela dépend je pense de si tes grilles sont indépendantes entre deux carrés définis?
Si tes grilles ne sont pas indépendantes (ex : 1er carré avec grille de i1j1 jusqu'à i10j10 et un deuxième carré juste à droite de i1j11 jusqu'à i10j20) alors c'est merdouilleux. ![]()
Sinon c'est probablement acceptable.
Pas certain de comprendre ce que veut dire H3bus, j'ai l'impression qu'il veut en fait que tu lisses la taille de tes cellules pour en avoir un nombre entier dans un carré. De toute façon le principe de l'erreur c'est que tu n'es pas capable de la corriger, autrement tu ne la ferais pas. ![]()
Mais bon par contre, même si tu n'as pas abordé, peut-être en effet que tu souhaites aussi avoir une grille contenant que des cellules complètes, auquel cas il faudra en effet lisser la différence entre la taille de ton carré et celle de nombre_cellules_entieres fois la taille de tes cellules en répartissant cette différence sur chaque cellule. Ce qui aura aussi pour incidence de répartir l'erreur uniformément entre tes différentes cellules.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 10-03-2017 à 10:02:36
Si une cellule pour être complète doit déborder de ma zone, c'est pas grave.
Les cellules de ma grille ne sont pas indépendantes. Pour rappel, je veux compter le nb de points qui se trouve dans chacune de ces cellules. Donc, je pense que l'erreur de précision que j'ai fait que je dois probablement comptabiliser des points dans une cellules qui devraient en fait être comptabilisé dans une des cellules adjacentes, d'où le décalage que j'observe entre ma cellule censé contenir le plus de points et le fait que ces points sont affichés à qq dizaines de mètres à côté (entre 20 et 50m, ça dépend de la taille de la zone étudiée et de la taille de chaque cellule) . ![]()
H3bus, j'ai pas compris ton algo. En plus, comme tu l'as peut-être vu, il faudrait, idéalement, que le calcul soit faisable via une simple requête SQL (c'est pour être plus rapide que par du calcul pur en PHP).
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 10-03-2017 à 12:17:43
Je ne parle pas de l'indépendance des cellules mais bien des grilles entières.
Par exemple si dans ton carré d'environ 1° de latitude et longitude tu as des cellules à droite mordues par le bord du carré, est-ce que si tu déplaces ton carré de 1° vers la droite tu dois repartir sur le complément de tes cellules mordues ou non? Parce que si tu repars sur tes cellules mordues ça veut dire que tu vas ajouter à chaque fois de l'erreur sur la précédente. Donc est-ce que ton étude se limite à ce carré de 1° de côté ou c'est juste une question de représentation des données?
Après c'est certain que le mieux serait de trouver sur quel modèle se base le WGS84, ça permettrait de faire le bon calcul et d'arrêter de se poser des questions. Mais de ce que semble dire wiki, ce serait un modèle simple d'ellipsoïde dont les paramètres sont donnés : https://fr.wikipedia.org/wiki/WGS_84
Et tout le problème réside dans le calcul d'un arc d'ellipse : https://fr.wikipedia.org/wiki/Ellip [...] C3.A9rence mais cela reste faisable, faut juste déterminer à quel ordre tu arrêtes ton développement.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 10-03-2017 à 16:47:26
Désolé, je n'ai pas assez réfléchit, la méthode par développement donne uniquement la circonférence complète (ou demi-circonférence ou quart-circonférence par symétries), pour pouvoir intégrer sur deux bornes quelconques c'est beaucoup plus compliqué. ![]()
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 10-03-2017 à 22:29:21
je ne sais pas si ça peut servir, mais postgres et oracle fournissaient déjà des calculs de distances sur sphères en 2005
je pense que sqlserver le fait aussi d'ailleurs maintenant avec leur types composites déjà disponibles depuis quelques années
je me suis servis des fonctions postgres pour effectuer des associations distances (fonction de coords gps) entre membres d'un site de rencontre en 2005, ça date ![]()
Message édité par bill_clinton le 10-03-2017 à 22:31:26
---------------
vente système facility management http://facilitymanagement.over-blo [...] eraux.html
Marsh Posté le 10-03-2017 à 23:47:29
Je suis sur MySQL. Le calcul de distance entre 2 points ne me pose pas de soucis. Comme indiqué, c'est additionner des distances à des coordonnées qui me pose soucis, en particulier quand ça conduit à des distances importantes > 1° d'arc.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 11-03-2017 à 04:40:32
pourtant c'est bien ce que tu dis,
"Comme indiqué, c'est additionner des distances à des coordonnées qui me pose soucis, en particulier quand ça conduit à des distances importantes > 1° d'arc."
ce que tu obtiens est facilement explicable par une bête erreur de calcul répétée plusieurs fois
regarde le code source de postgres vu que tu n'auras pas le code d'oracle, mais cette fonction est la bonne visiblement
Message édité par bill_clinton le 11-03-2017 à 04:43:32
---------------
vente système facility management http://facilitymanagement.over-blo [...] eraux.html
Marsh Posté le 11-03-2017 à 04:49:18
est'ce que tu n'aurais pas choisi toi même une constante au hasard ?
dans ce cas là il faut minimum 10-9 decimales et encore faut-il que ta constante soit bien définie (c'est à dire calculée)
sinon tu n'auras jamais de résultats pouvant exister dans la réalité c'est évident
si tu veux te refaire tout le boulot qui été fait sur ces fonctions postgre ou oracle, libre à toi
ici, ça devrait être plus simple pour découper ta sphère en ce que tu veux : ![]() http://myriam.collenne.free.fr/3_spheres.htm
http://myriam.collenne.free.fr/3_spheres.htm
à mon avis, il va falloir voir du côté des ellipses
Message édité par bill_clinton le 11-03-2017 à 05:29:51
---------------
vente système facility management http://facilitymanagement.over-blo [...] eraux.html
Marsh Posté le 11-03-2017 à 05:25:18
ou alors installes toi postgres ou oracle
---------------
vente système facility management http://facilitymanagement.over-blo [...] eraux.html
Marsh Posté le 11-03-2017 à 12:35:37
Bon le calcul de la longueur d'un arc d'ellipse est accessible à un BAC S et est très bien décrit ici : http://serge.mehl.free.fr/anx/int_elli.html (cas "2ème espèce" )
Il ne faut pas passer par l'intégrale de Wallis mais en intégrant terme à terme la série développée :
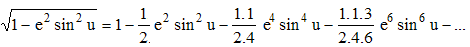
Pour cela il faut passer chaque sin^n(u) sous la forme d'Euler ( http://serge.mehl.free.fr/chrono/Moivre.html#lin ) puis linéariser le tout, une fois ramenés à des fonctions trigo à la puissance 1 tu peux les intégrer.
Alors perso je me suis arrêté au premier ordre du développement avec sin²(u), ça m'a déjà assez saoulé comme ça. ![]()
Mais une fois intégré si je prends des bornes d'intégration de 0 jusqu'à 2*pi je tombe 40 075 km de circonférence*, et j'arrive à voir des différences de longueur d'arc entre les bornes [0°;1°] et [44°;45°]. Pour bien faire, je pense qu'il faut que tu ailles jusqu'à l'ordre 3 et donc te taper le sin^2(u), le sin^4(u) et le sin^6(u) à linéariser puis à intégrer. ![]()
Bon courage. ![]()
(*) en utilisant les paramètres a et e (faut calculer e en fonction de a et f) de https://fr.wikipedia.org/wiki/WGS_84
Message édité par MaybeEijOrNot le 11-03-2017 à 12:42:42
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 11-03-2017 à 22:43:50
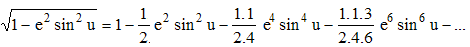
Chat Pi Tau ! ![]()
ça à l'air amusant comme formule infinie ![]()
Message édité par bill_clinton le 11-03-2017 à 22:45:10
---------------
vente système facility management http://facilitymanagement.over-blo [...] eraux.html
Marsh Posté le 13-03-2017 à 13:28:20
Pour la circonférence, j'utilise bien la valeur 40075 km.
https://fr.wikipedia.org/wiki/WGS_84 -> ça sert à quoi le coeff d'aplatissement f ![]() Dans quelle formule on peut l'utiliser ?
Dans quelle formule on peut l'utiliser ?
Pour le coup des intégrales, je sens que ça va être chaud ![]()
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 13-03-2017 à 13:55:26
Si tu veux je peux décrire de manière plus formelle l'algo que j'ai exposé de manière dégueu quelques post plus haut.
Mais à la réflexion je ne sais pas si il mène au résultat que tu souhaites. Son but est d'obtenir un nombre identique de points par latitude de ta grille, malgré le fait que la longueur d'arc en longitude dépende de la latitude.
Le principe et de travailler en "pas angulaires" pour générer la grille au lieu d'utiliser les distances.
Au final on obtiendrait un effet "d'étirement horizontal":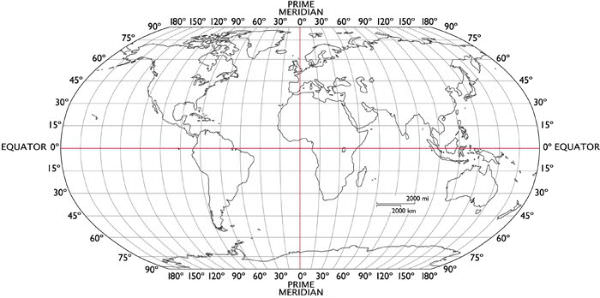
Message édité par h3bus le 13-03-2017 à 14:13:07
---------------
sheep++
Marsh Posté le 13-03-2017 à 15:53:04
Tu peux toujours me mettre ton algo. Travailler par pas angulaire ou par distance par rapport à un point, ça peut être la même chose à partir du moment où le pas angulaire correspond bien à la distance souhaitée. Ce pas angulaire sera donc variable si je ne dis pas de bêtise.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 13-03-2017 à 16:35:38
Justement le pas angulaire est fixe, il est calculé une fois pour générer le moins d'erreur possible.
Cela va engendrer une erreur sur les distances de la grille du fait de la projection.
L'algo
Pour simplifier les notations
- φ = angle de latitude
- λ= angle de longitude
On se donne une "boite" définie par ses deux coins opposés (φ1, λ1) et (φ2, λ2). On peut dors et déjà noter que cette boite n'en est pas une dès qu'on la projette.
On se donne un pas de grille δG, qui est la distance cible entre deux points adjacent sur une longitude ou latitude.
On se dote de deux fonctions de clacul de distance
- la longueur de l'arc à longitude fixe: Dlong(φ1, φ2)
- la longueur de l'arc à latitude fixe, pour une latitude donnée: Dlat(φ, λ1, λ2)
On calcule le nombre d’occurrences du pas de grille dans la longitude de la boite:
Nφ = Dlong(φ1, φ2) / δG
On en déduit le pas d'angle en longitude:
δφ = (φ2 - φ1) / Nφ
On calcule la latitude médiane de la "boite"
φm = (φ1 + φ2) / 2
On calcule le nombre d’occurrences du pas de grille à la latitude médiane:
Nλ = Dlat(φm, λ1, λ2) / δG
On en déduit le pas d'angle en latitude:
δλ = (λ2 - λ1) / Nλ
En suite on génère les point en itératif séparés de (δφ, δλ)
λc = λ1
Tant que λc < λ2:
φc = φ1
Tant que φc < φ2:
Point de grille (φc, λc)
φc += δφ
λc += δλ
---------------
sheep++
Marsh Posté le 13-03-2017 à 17:43:00
"Cela va engendrer une erreur sur les distances de la grille du fait de la projection." -> c'est ce que fait ton algo ?
Parce que c'est le pb que j'ai justement.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 13-03-2017 à 20:45:40
Attention, le message qui va suivre présente des dangers pouvant conduire au suicide mental !
Pour moi, H3bus lisse l'erreur faite entre une distance calculée au coin supérieur gauche et une distance calculée au coin inférieur droite de ta grille. Cela suppose de faire une erreur, or, avec un modèle sphérique, quelque soit l'angle tu obtiens la même longueur d'arc et donc aucune erreur. Je ne vois pas l'intérêt de travailler en angle plutôt qu'en distance, pour moi son idée réside dans le fait de travailler avec des distances calculées à partir des coordonnées du centre de la grille si je ne m'abuse. Mais dans tous les cas, cela n'a de sens que si tu travailles avec des longueurs d'arc variables en fonction de la latitude et de la longitude et donc un autre modèle que le modèle sphérique.
C'est ce qu'est le modèle WGS84, au lieu de définir la terre comme une sphère, il la définit comme une ellipsoïde. Une sphère peut être décrite par un seul paramètre qui est le rayon, un ellipsoïde par deux paramètres qui sont le demi-grand axe (a qui est la distance entre le centre et l'équateur) et l’aplatissement (f). Ces deux paramètres te permettent de calculer le demi-petit axe (b qui est la distance entre le centre et un pôle) et les excentricités (e et e') selon les formules suivantes :
_______________________________
a*f = a-b
b = a-a*f
_______________________________
_______________________________
e = racine[(a²-(a-a*f)²)/(a²)]
_______________________________
_______________________________
e' = racine[(a²-(a-a*f)²)/(a-a*f)²]
_______________________________
Jusque là, rien de bien compliqué, tu remarqueras sur wiki que seuls les valeurs de a et f sont données avec un égal, les autres sont données avec un "un peu près égal", parce que c'est un résultat arrondi obtenu par les calculs précédents.
Maintenant que tu as tes paramètres associés a et e, b et e' tu peux passer au calcul des distances entre deux angles selon la formule :
où :
a = a ou b
e = e ou e'
0 et t sont les bornes et donc correspondent à φ1 et φ2 ou λ1 et λ2
Petit rappel, l'intégrale de u.du correspond à la primitive de u pour le borne supérieure moins la primitive de u pour la borne inférieure.
Ex :
Calculons l'intégrale de 3 à 4 de 2x.dx
On recherche la primitive de 2x qui est x²
On soustrait la borne inférieure à la borne supérieure : 4²-3² = 16 - 9 = 7
Rien de sorcier dans cet exemple. Le problème c'est que dans l'intégrale donnée pour l'ellipsoïde il y a un terme dont on ne connait pas la primitive : racine(1-e².sin²u).du
Mais grâce aux développements en série, on sait que ce terme équivaut à :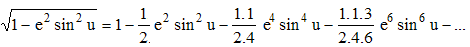
Et ça on connait presque la primitive, les constantes on sait faire, il y a juste les sin^n(u) qu'on ne sait pas faire, la puissance nous gêne. ![]()
Mais encore une fois, il existe une solution détournée qui est de passer par la forme d'euler de cette fonction trigo :
Alors "int" ça ne veut pas dire "integer" mais bien i (nombre complexe dont i²=-1) multiplié par n (constante) multiplié par t (variable, qui dans notre cas est u). ![]()
Ex :
sin²(u) = [(e^(i.u)-e^(-i.u))/(2.i)]²
On développe très tranquilou :
[(e^(i.u)-e^(-i.u))/(2.i)]² = [e^(i.u)-e^(-i.u)]² / [(2.i)]²
= [e^(2.i.u) + e^(-2.i.u) - 2.e^(i.u-i.u)] / [(2.i)]² (a-b)² = a² + b² - 2.a.b ![]() (pour les autres puissances tu as le binôme de Newton)
(pour les autres puissances tu as le binôme de Newton)
= [e^(2.i.u) + e^(-2.i.u) - 2.e^0] / [(2.i)]²
= [e^(2.i.u) + e^(-2.i.u) - 2] / [(2.i)]²
= [e^(2.i.u) + e^(-2.i.u) - 2] / [4.i²]
= [e^(2.i.u) + e^(-2.i.u) - 2] / [-4]
= (-1/2).[(e^(2.i.u) + e^(-2.i.u)) / 2] + 1/2 On reconnait le terme [(e^(2.i.u) + e^(-2.i.u)) / 2] qui vaut cos(2.u)
= (-1/2).cos(2.u) + 1/2
= -cos(2.u)/2 + 1/2
Maintenant on cherche la primitive de ce terme :
cos(2.u) --> (1/2).sin(2.u)
1/2 --> u/2
La primitive de sin²(u) est donc : (-1/4).sin(2.u) + u/2
Sauf que nous on cherchait la primitive de : [1 - (1/2).e².sin²(u)].du
Soit : u - (1/2).e².[(-1/4).sin(2.u) + u/2]
u - u.e²/4 + (e².sin(2.u))/8
Et là on peut calculer l'intégrale de 0 à 2.pi (ou autres bornes mais celle à 0 évite déjà un calcul puisque ça donnera 0), ce qui donne :
I = 6,27259893
d = a*I = 40007495 m
Circonférence terre à l'équateur = 40 007 km
Bon la dernière fois, j'avais réussi à trouver 40 075 km, mais là je n'ai plus les idées claires pour débugger. Soit j'ai fait une faute ici ou avant, soit je me plante entre les couples (a et e) et (b et e'). Faut dire que j'ai tout fait dans l'éditeur de message du forum sauf les calculs numériques. Mais attention, j'ai arrêté mon intégration au second terme du développement limité qui est -(1/2).e².sin²(u), plus on augmente l'ordre du développement, plus on augmente la précision, c'est pourquoi je disais qu'il faudrait t'arrêter à un ou deux ordres de plus.
Tout ça pour dire que c'est faisable, mais c'est très lourd, néanmoins une fois que tu as ta formule c'est bon. Si tu as de la chance tu arriveras peut-être à la trouver sur le net mais j'en doute.
Les calculs écrits comme ça c'est un peu moche désolé, mais je n'allais pas m'amuser à les écrire sur Word pour en faire des images.
Alors c'est clair que sorti de BAC S la plupart ne doivent pas prendre assez de recul et prendre peur mais normalement toutes les notions sauf les développements limités (mais il est donné ici) sont vues avant le BAC et réutilisées dans le supérieur. Sans la pratique il faut clairement remettre à jour des notions je pense mais normalement si ça avait été assimilé une fois ça devrait pouvoir ressortir une seconde fois. ![]()
Message édité par MaybeEijOrNot le 13-03-2017 à 21:34:44
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 13-03-2017 à 22:53:31
Bon ok j'ai bon, c'est écrit sur wiki :
| Citation : la longueur de l'ellipse méridienne est : 40 007,863 km (via la formule approchée 2·π.(a+b).(1+ e4/64+ ...)) |
![]()
Ils utilisent la formule venant de l'intégrale de Wallis, ce qui ne permet pas d'intégrer sur des bornes quelconques. Ils prennent la moyenne de a et b, donc il y a une erreur dans la formule entre parenthèses, ils ne devraient pas multiplier par 2 avant pi. Mais je ne comprends pas le sens non plus de prendre la moyenne de a et b...
Comme ça rendait dingue de ne pas comprendre mon erreur j'ai fait le sin^4(u), ça se fait super bien au binôme de Newton et les primitives aussi ça va vite une fois que tu as compris.
J'ai donc une différence de distance entre 0° et 1° et entre 44° et 45° de 476m.
Et entre 43° et 44° et entre 44° et 45° une différence de 9m.
Ce qui veut grossomodo dire une différence de 4,5m sur 1°, et si tu prends par rapport au centre de la grille ça donnerait 2m de chaque côté. Et si tu lisses ça sur toutes tes cellules ça devient négligeable.
Formule cadeau si je ne me suis pas planté :
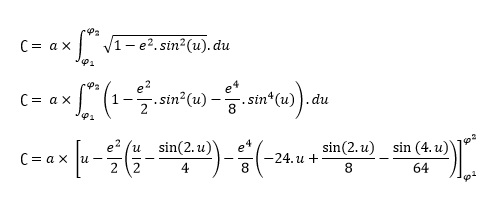
Sinon personne n'a fait Maths/Info ici? Cela nous aiderait surement plus.^^
Message édité par MaybeEijOrNot le 13-03-2017 à 22:54:58
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 13-03-2017 à 23:14:25
Peut-être que j'ai tort, mais mon avis est qu'il y a une erreur dans l'énoncé, car il est impossible de projeter une grille de pas fixe (en distance) sur une sphère.
Ou alors la définition de ladite grille doit être définie plus précisément.
---------------
sheep++
Marsh Posté le 13-03-2017 à 23:28:14
MaybeEijOrNot, merci pour tes posts très complets ! J'ai bien compris le raisonnement et tes calculs. Maintenant, je me demande si je vais me lancer là-dedans pour une erreur de finalement 20 à 30m.
h3bus : oui, c'est vrai que vouloir projeter une grille de pas fixe sur un sphère quand on commence à la faire sur plusieurs km, ça peut générer des pbs de déformation... ![]()
En tout cas, merci à tous pour votre participation. Je vois que finalement, mon pb n'est pas si simple...
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 14-03-2017 à 10:48:11
Après il y a en effet le problème de projection qui conduit à l'obtention de "rectangles" qui ne sont pas des rectangles.
Sinon je crois avoir trouvé la formule développée jusqu'à l'ordre 4 : https://fr.wikipedia.org/wiki/Arc_de_m%C3%A9ridien
Mais c'est vrai que quand tu fais des recherches sur Internet tu tombes généralement sur des distances calculées avec Pythagore, parfois ils te disent que c'est une approximation trop médiocre et qu'il faut calculer l'arc de cercle à partir d'un modèle sphérique mais très rarement on te parle de l'ellipsoïde et encore moins on détaille le calcul. Donc comme tu dis, est-ce que ça vaut le coup?
Sachant que dans ce que je te propose on reste avec ds approximations, on supposera constantes les distances d'un degré d'arc sur le domaine étudié. Sinon après faut passer sur de l'intégrale double ou triple. ![]()
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 14-03-2017 à 11:10:12
Moi, effectivement, je travaille avec un modèle sphérique non une ellipsoïde, d'où mes écarts quand je travaille sur des petites distances. Sur des grandes, ces écarts de qq dizaines de mètres ne se voient pas. Mais dans le cas de figure que j'ai traité dernièrement, les infos de localisation que j'avais étaient précises. Du coup, c'est là qu'est apparu les écarts. C'était flagrant.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 14-03-2017 à 11:16:45
J'ai regardé ton lien : si j'ai bien compris, B représente la distance entre l'équateur et un point se situant à une certaine latitude. Du coup, si j'ai un point et une distance, il faut résoudre l'équation pour trouver la latitude ![]()
En plus, comme c'est pas par rapport à l'équateur que je travaille mais par rapport à un autre point, il faudra soustraire les 2 distances par rapport à l'équateur pour avoir la distance entre les 2 points, non ?
Ca me paraît vraiment hardcore ![]()
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 14-03-2017 à 13:59:47
Le dernier lien, reprend juste ce que j'ai écrit précédemment, simplement moi je t'ai donné la formule arrêtée à l'ordre 2 et sur cette page wiki ils te donnent la formule arrêtée à l'ordre 4.
L'équateur ça correspond à un angle de 0° donc après si tu veux faire par rapport à un autre point alors oui il faut soustraire. Mais c'est le principe d'une intégrale : borne supérieure moins bonne inférieure. Et quand la borne inférieure vaut 0 tu fais juste la borne supérieure puisque tu dois lui soustraire 0...
Ce que tu me dis c'est que pour avoir AB tu devras faire OB-OA soit (B-0) - (A-0), ce qui revient en fait à faire B-A.
Je partais du fait que tu avais les coordonnées et donc que tu n'avais pas besoin de recalculer des coordonnées. Parce que oui la fonction inverse risque d'être encore plus galère.
Je ne pense pas qu'il existe de solution simple à ton problème si ce n'est d'accepter l'erreur commise en basant tes calculs sur un modèle sphérique là où Google utilise un modèle d'ellipsoïde.
Message édité par MaybeEijOrNot le 14-03-2017 à 14:03:27
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 14-03-2017 à 14:04:16
Comme indiqué, j'ai les coordonnées d'un point et je veux, à partir de ce point, calculer les coordonnées des autres points qui vont être séparés en "vertical" et "horizontal" d'une certaine distance : ces points vont alors former les coins de la grille (je ne les relie pas entre eux en diagonal, uniquement reliés en vertical et horizontal). Du coup, ça va être chaud.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 14-03-2017 à 14:19:02
Oui mais ça ne change rien, dans ce que j'ai compris de ce que tu voulais faire. Il te suffit d'avoir les coordonnées du coin supérieur gauche, les coordonnées de tes points puis de calculer la distance longitudinale et latitudinale (?) entre ton point et ton coin.
Ex :
Coin(φ0;λ0)
Point(φ1;λ1)
Tu calcules l'arc de cercle entre φ0 et φ1, ça te donne disons 150m.
Tu calcules l'arc de cercle entre λ0 et λ1, ça te donne disons 30m.
Tu en déduis que ton point est situé dans la cellule de la première ligne et 3ème colonne (j'inverse peut-être colonne et ligne parce que je suis toujours paumé entre les latitudes et longitudes mais osef) où chaque cellule fait 55m de côté.
Ce n'est pas ça que tu veux faire?
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 14-03-2017 à 14:54:28
Je ne veux pas calculer les distances longitudinales et latitudinales entre les points qui composent les coins des cellules de la grille, je veux faire l'inverse. Je veux calculer les coordonnées de ces points à partir d'un point de référence et d'une distance. En fait, j'ai déjà un pb pour définir les coordonnées des coins des cellules de ma grille.
Après oui, effectivement, pour savoir à quelle cellule appartient un point à comptabiliser, ta formule va me servir ![]()
Message édité par rufo le 14-03-2017 à 15:00:56
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 14-03-2017 à 15:19:02
Tu veux aussi représenter ton maillage si je comprends bien?
Dans ce cas là tu délimites ta zone (un carré de 1° de côté si j'ai bien suivi), tu calcules la longueur (en arc de d'ellipse) des côtés de ce carré (qui va devenir un rectangle). Tu divises cette longueur par la longueur des cellules. Tu vas obtenir environ 2018 cellules (cela dépendra de la latitude et de la longitude à laquelle se trouve la zone). À partir de là tu vas faire l'approximation qu'une cellule fera 1°/2018 de longueur et tu obtiens les coordonnées de chaque cellule en itérant.
C'est déjà ce que tu faisais avant mais avec des longueurs d'arc de cercle, non?
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 15-03-2017 à 10:29:14
Oui, c'est ça. Précision : la taille de ma grille est paramétrable. Elle peut faire 60 NM de côté mais ça peut être moins. La taille des cellules est aussi paramétrable (cellules carrées) : c'est 0.03 NM (soit 55.56 m) mais ça peut être moins comme ça peut être plus.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Sujets relatifs:
- [Wordpress] Afficher article(s) sur Facebook
- creer un projet a partir des infos debug
- lancer vidéos à partir d'une page HTML en local, c'est possible ?
- Afficher plusieurs lignes sur une seule
- OpenLayers3 : afficher Text
- afficher des images au fur et à mesure d'un appel ajax
- [VB.NET] Créer un formulaire a partir d'une classe
- Interface Swing à partir d'un tableau 2D (jeu)
- Java : Problème affichage à partir d'un dossier txt
- Convertir fichier PDF en txt à partir d'un fichier d'initialisation




Marsh Posté le 08-03-2017 à 16:19:33
Bonjour à tous,
Voilà, je veux tracer dans GoogleEarth une grille (faite de rectangles) à partir d'un point et d'un "pas" exprimé en mètres. J'ai un soucis pour trouver la formule exacte qui permet de calculer les coordonnées des points composants les coins des rectangles composant cette grille à partir de mon point d'origine et du pas.
Genre, j'ai un point A avec des coordonnées exprimées en WGS84 (en décimales) et un pas de 55m. Je veux avoir les coordonnées des coins de chaque rectangle (en fait, un carré) ayant 55m de côté qui va composer ma grille.
En fait, je n'arrive pas à trouver la valeur à ajouter à la latitude et longitude de mon point d'origine pour me décaler de mon pas (ici, 55m).
J'ai mis ça : $Step = $radius * 0.621371192 * 0.000014483; // $radius in meters
Mais ça ne colle pas tout à fait. J'ai des rectangles et non des carrés et ils ne font que 36m en largeur. En longueur, c'est bon.
Merci.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta